GIS空间数据库（16）R树索引

R树索引是一种高效的空间索引，它是B树在多维空间的扩展，也是平衡树。R树的结构类似于B+树的平衡树。

R树及其特点

对于一棵M阶的R树，R树中每个非叶子结点都由若干个(p，MBR)数据对组成。MBR(Minimal Boundary Rect)为包含其对应孩子的最小边界矩形。这个最小外接矩形是个广义上的概念，二维上是矩形，三维空间上就是长方体MBV(Minimum Bounding Volume)，以此类推到高维空间。p是指向其对应该子结点的指针。

叶子结点则是由若干个(OI，MBR)组成，其中MBR为包含对应的空间对象的最小外接矩形。OI是空间对象的标号，通过该标号可以得到对应空间对象的详细的信息。

R树查找

伪代码如下：

Algorithm R_Search(N,W) {
    /*在根结点为N的R树中查找所有与W相交的数据矩形*/

    if (N.LEVEL==0) //N是叶子结点
        //  Return all data rectangles that intersect with W；
    else //N不是叶子结点
        for (i=1;i<N.COUNT;i++)
            if (N.MBRi;Intersect with W)
              R_Search (N.pi,W);
}

R树插入

伪代码如下：

Algorithm R_Insert(N,P){
/*向根结点为N的R树中插入数据矩形P*/
  if (N.LEVEL==0) {
        Insert P into N;
        if (N overfill) Split N;
    }
  else {//N是中间结点
      // Choose the entry in N whose rectangle needs 
      // least area enlargement to include the new data rectangle.
      // Resolve ties by choosing the entry with the rectangle of
      // smallest area (Let's suppose it's entry is the answer)
      R_Insert(N.pi,P);
      // Adjust N.MBRi to enclose all rectangle in its child node；
    }
}

R树删除

伪代码如下：

Algorithm R_Delete(N,P){
/*从根结点为N的R树中删除数据矩形P*/
  if (N：LEVEL==0) 
  {//N是叶结点
      if (N包含P)
      {
          // 从N中删除P
          N.COUNT=N.COUNT-1;
          return true;
      }
      else
          return false;
  }
  else
  {
      for (i =1;i<N.COUNT;i++)
          if (N.MBRi intersects with P)
            if (R_Delete(N.pi,P))
                if (N.pi,COUNT=m)
                    // Adjust N.MBRi to enclose all child's rectangles；
                else
                {
                    // Reinsert all remain entries of N.pi and delete N.pi；
                    // if N underfilled， Reinsert alI         
                    // remain entries of it and
                    // delete it too...；〗
                }
  }
}

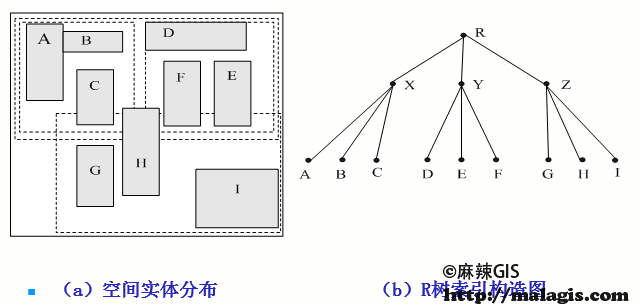
地图对应的R树结构

最后编辑：2019-09-16

作者：acer

这个作者貌似有点懒，什么都没有留下。

站内专栏