KD树定义
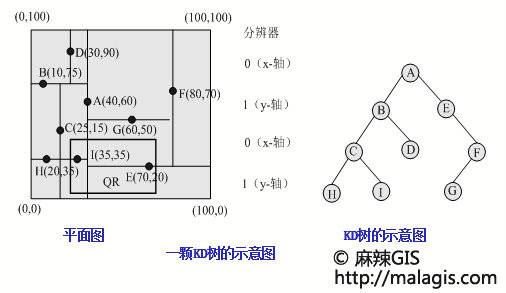
KD树的每个内部结点都包含一个点,每个结点表示k维空间中的一个点,并且和一个矩形区域相对应,树的根结点和整个研究区域相对应。KD树要求用平行于坐标轴的纵横分界线将平面分为若干区域,使每个区域中的点数不超过给定值。树中奇数层次上的点的x坐标和偶数层次上的点的y坐标把矩形区域分成两部分。分界线仅起分界的作用,它的选取没有硬性的限制。一般选用通过某点的横向线或者纵向线。分界线上的点,对左右分界线来说属于右部,对上下分界线来说属于上部。 如图:
KD树查找
伪代码
Algorithm KD_Search(R,P)
/*在根结点为R的KD树(子树)中查找点P。找到则返回结点,否则返回NULL*/
Begin
If R=NULL Then Return NULL;//Not Found
If R. Point=P Then Return R;//Found;
Else
Begin
d:=Discriminator of R;
If P[d] <R Point[d] Then /*比较P点与R结点的第D维的值*/
KD_Search(R.Lchild,P)//在左子树继续查找
Else
KD_Search(R.Rchild,P)//在右子树继续查找
End
End.
KD树插入
伪代码
Algorithm KD_Insert(R,P,F)
/*在根结点为R的KD树(子树)中插入点P,F为R的父结点*/
Begin
If R=NULL Then
Begin
Create a Node P;
If F=NULL Then //KD树为空
Root:=P//P成为根结点
Else
If R Is the Left child of F Then
F.Lchild:=P//P作为F的左孩子
Else F.Rchild:=P//P作为F的右孩子
End
Else
Begin
d:=Discriminator of R;
If P[d]R.Point[d] Then/*比较P点与R点的第D维的值*/
KD_Insert(R.Lchild,P,R)//插入到左子树中
Else
KD_Insert(R.Rchild,P,R)// 插入到右子树中
End;
End;
KD树删除
Algorithm KD_Delete(R,P)
/*在根结点为R的KD树(子树)中点P,删除成功返回True,否则返回False */
Begin
Q:= KD_Search(R,P);//Q为要删除的对象
LABEL;
If Q=NULL Then Return False;//Not found
If (Q.Lchild=NULL) And (Q.Rchild=NULL) Then
Begin//第一种情况
F:=Q is Father Node;
If Q is the left Child of F then
F.Lchild:=NULL
Else F.Rchild:NULL;
Delete Node Q;
Return True;
End
Else
Begin
If (Q.Rchild=NULL) Then第三种情况转化为第二种情况处理
Q.Rchild:=Q.Lchild;
M:=FindMin(Q.Rchild);
(Q)←(M);//将M结点的值赋给Q结点
Q:=M;//让Q指向M结点
GOTO LABEL;//继续删M结点
End
end
- 本文固定链接: https://www.chtfs.com/4483/
- 转载请注明: acer 于 测绘途夫 发表